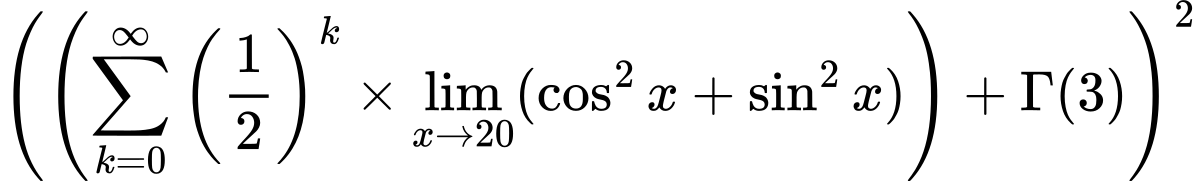x
Mobile Notice
You appear to be on a device with a narrow screen width (i.e you are probably on a mobile device). Due to the nature of mathematics on this site, it best views in landscape mode. On narrow screens, some math expressions may run off the side of the screen (you should be able to scroll to see them)
num2math
A math expression generator.
What is a complicated math
equation that equals x? Let's find out!
10 Hard & Complicated Equations for 16
Here are some pre-generated hard and complicated equations that equal 16. These random math formulas are perfect for challenges. Copy the LaTeX code or use our generator above for more.
Variation 1
${ \left({{\lim_{x \to 0}{ {-\ln(1 + 2(e^{-x} - 1))} \over {x} }} - {\lim_{x \to 21} {{x^2 - 9} \over {x - 3}}}}\right) \left({\left({{\lim_{x \to 0} {{x^2 - 81} \over {x - 9}}} - \lim_{{x\to 17}}(\cos^2x + \sin^2x)}\right) + {\sum\limits_{k=0}^\infty {\left({23 \over {24}}\right)^{k}}}}\right) + {{-24e^{\pi i}}}{\left({\left({{-9e^{\pi i}} - \lim_{{x\to 14}}(\cos^2x + \sin^2x)}\right) - {\prod_{k=1}^{2} k} + {\lim_{x \to 0}{ {-\ln(1 + 24(e^{-x} - 1))} \over {x} }}} \right)} }$
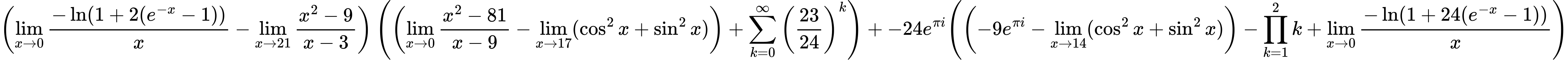
Variation 2
${ {\left({\lim_{x \to 0}{ {e^x - 1} \over {x} }}\right)}^2 + {{\prod_{k=1}^{2} k}}{\left({\prod_{k=1}^{1} k}\right)}{\left({\lim_{x \to -6} {{x^2 - 81} \over {x - 9}}}\right)} + {\left({\lim_{x \to \infty}{{ 15x^{4} + 11x } \over {{ 5x^{4} - 7x }}}}\right)}^2}$
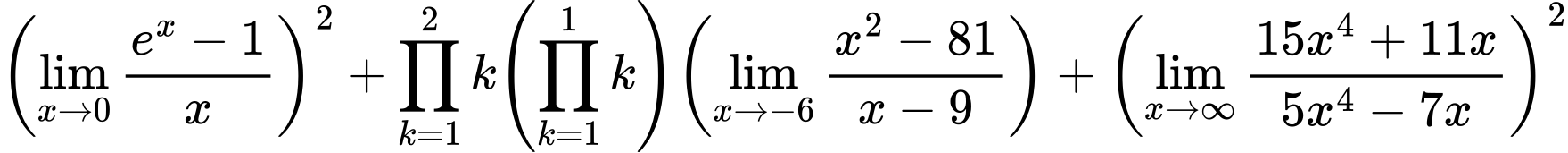
Variation 3
${\lim_{x \to -5} {{x^2 - 49} \over {x - 7}}} \times {{\prod_{k=1}^{3} k}} + {\sum\limits_{k=0}^\infty {\left({3 \over {4}}\right)^{k}}}$
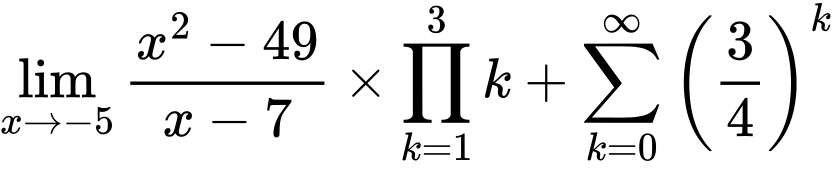
Variation 4
${\lim_{x \to \infty}{x^{1/x}}} \times {{\lim_{x \to 0}{ {e^{9x} - 1} \over {x} }}} + {\lim_{x \to 16} {{x^2 - 81} \over {x + 9}}}$
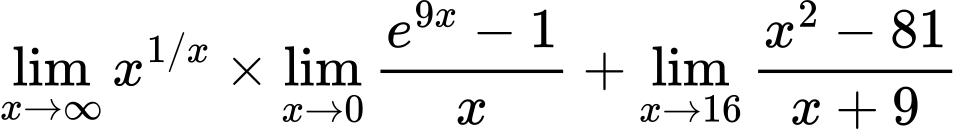
Variation 5
${ {\left({\lim_{x \to 0}{ {e^x - 1} \over {x} }} + {\sum\limits_{k=0}^\infty {\left({2 \over {3}}\right)^{k}}}\right)}^2}$
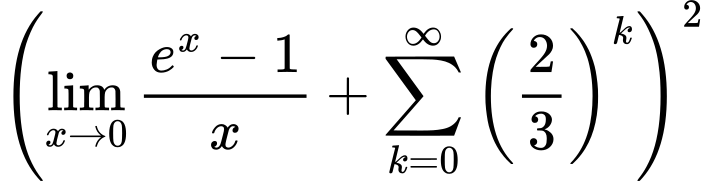
Variation 6
${{\left({{\sum\limits_{k=0}^\infty {\left({7 \over {8}}\right)^{k}}}}\right)}{\left({{\lim_{x \to 0}{ {-\ln(1 + 2(e^{-x} - 1))} \over {x} }}}\right)}}$
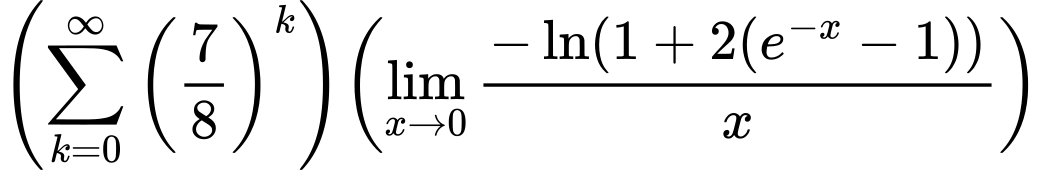
Variation 7
${\lim_{x \to 0}{ {e^x - 1} \over {x} }} \times {\left({{\lim_{x \to \infty}{{ 22x^{4} - 3x^{3} + 9x^{2} - 11x } \over {{ 2x^{4} + 7x^{2} + 11x }}}} \over {\lim_{{x\to 14}}(\cos^2x + \sin^2x)}}\right)} + {\lim_{x \to 13} {{x^2 - 64} \over {x + 8}}}$
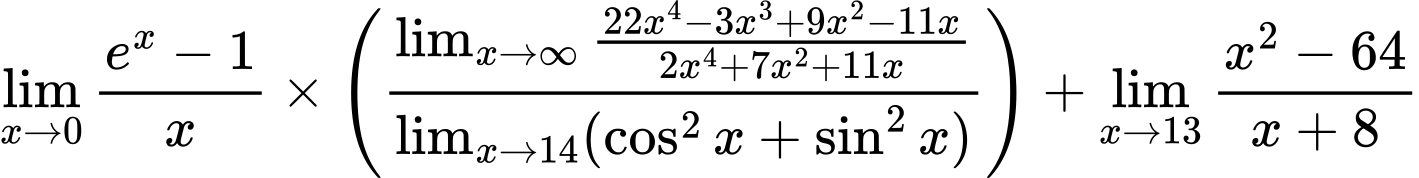
Variation 8
${ \left({{\sum\limits_{k=0}^\infty {\left({15 \over {16}}\right)^{k}}} - {\Gamma (4)}}\right) \left({{\lim_{x \to 0}{ {e^x - 1} \over {x} }} + \left({{\lim_{x \to 4} {{x^2 - 9} \over {x - 3}}} - \lim_{{x\to 2}}(\cos^2x + \sin^2x)}\right)}\right) + {{\lim_{x \to 0}{ {-\ln(1 + 6(e^{-x} - 1))} \over {x} }}}{\left({{\lim_{x \to 0}{ {e^x - 1} \over {x} }} - {\lim_{x \to 12} {{x^2 - 16} \over {x - 4}}} + {\lim_{x \to 0}{ {-\ln(1 + 6(e^{-x} - 1))} \over {x} }}} \right)} }$
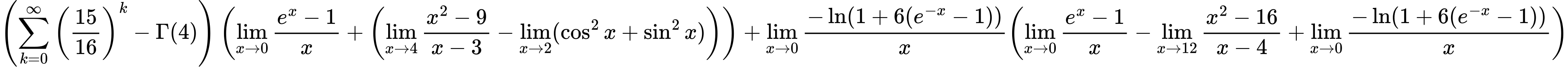
Variation 9
${ \left({{\lim_{x \to \infty}{{ 6x^{2} + 5x } \over {{ 3x^{2} - 2x }}}} - {\lim_{x \to 17} {{x^2 - 81} \over {x + 9}}}}\right) \left({{\lim_{x \to 0}{ {-\ln(1 + 8(e^{-x} - 1))} \over {x} }} + {\lim_{x \to 0}{ {-\ln(1 + 8(e^{-x} - 1))} \over {x} }}}\right) + {{\sum\limits_{k=0}^\infty {\left({7 \over {8}}\right)^{k}}}}{\left({{\lim_{x \to \infty}{{ 16x^{4} - 4x } \over {{ 2x^{4} + 8x^{2} + 11x }}}} - {\lim_{x \to 0}{ {e^{2x} - 1} \over {x} }} + {\sum\limits_{k=0}^\infty {\left({7 \over {8}}\right)^{k}}}} \right)} }$
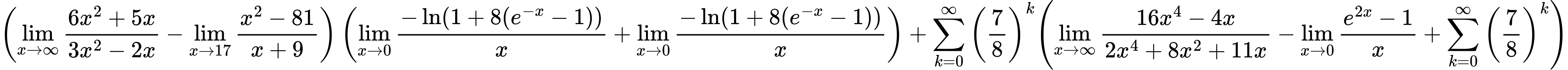
Variation 10
${ {\left(\left({{\sum\limits_{k=0}^\infty {\left({1 \over {2}}\right)^{k}}} \times \lim_{{x\to 20}}(\cos^2x + \sin^2x)}\right) + {\Gamma (3)}\right)}^2}$